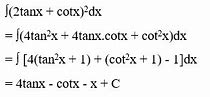
Cotx 2 Đạo Hàm

Dưới đây là bảng công thức đạo hàm, đạo hàm lượng giác, các hàm lượng giác và công thức đạo hàm cao cấp đầy đủ nhất giúp các bạn dễ dàng ôn lại những kiến thức toán học về đạo hàm đã được học một cách nhanh nhất để giải bài tập nhanh hơn, hiệu quả hơn.

Bảng đạo hàm của các hàm số cơ bản

Nếu u và v là các hàm khả vi n lần thì: với kí hiệu tổ hợp chập k của n phần tử

Cách tính đạo hàm bằng định nghĩa

Để tính đạo hàm của hàm số tại điểm bằng định nghĩa ta có quy tắc sau đây:

Bước 1: Giả sử ∆x là số gia của đối số tại x0, tính:

Mối liên hệ giữa sự tồn tại đạo hàm và tính liên tục

Định lí: Nếu hàm số có đạo hàm tại điểm thì liên tục tại .

Chú ý: Định lí trên chỉ là điều kiên cần, tức là một hàm có thể liên tục tại điểm nhưng hàm đó không có đạo hàm tại .

Đạo hàm của hàm số tại điểm là hệ số góc tiếp tuyến tại điểm đó.

Ta có phương trình tiếp tuyến tại điểm M:

Giả sử là các hàm số có đạo hàm tại điểm thuộc khoảng xác định. Ta có:

Bằng phương pháp quy nạp toán học ta có một số công thức đạo hàm mở rộng như sau: