Tổng 2 Vecto Có Hướng

Bài viết Công thức tính Tích vô hướng của hai vecto trong không gian với phương pháp giải chi tiết giúp học sinh ôn tập, biết cách làm bài tập Công thức tính Tích vô hướng của hai vecto trong không gian.

Công thức tính Tích vô hướng của hai vecto trong không gian (cực hay)

Bài giảng: Các dạng bài tập hệ trục tọa độ trong không gian - Cô Nguyễn Phương Anh (Giáo viên VietJack)

Bài 1: Trong không gian với hệ trục tọa độ Oxyz, cho các vecto a→=(1;2;1),

b→=(3;-1;2), c→=(4; -1; -3),d→=(3; -3; -5),u→=(1;m;2),m∈R.

b) So sánh a→.(b→.c→) và (a→.b→ ) c→

c) Tính các góc (a→,b→ ), ( a→+b→,3a→- 2c→ )

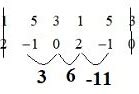
c→ =(4; -1; -3)⇒2c→ =(8; -2; -6)⇒ a→ -2c→ =(-7;4;7)

⇒b→ (a→ -2c→ )=3.(-7)-1.4+2.7=-11

b) b→ .c→ =3.4+(-1).(-1)+2.(-3)=7⇒a→ .(b→ .c→ )=(7;14;7)

a→ .b→ =3⇒(a→ .b→ ) c→ =(12; -3; -9)

Vậy a→ .(b→ .c→ )≠(a→ .b→ ) c→

+ a→+ b→=(4;1;3),3a→- 2c→=(-5;8;9)

d) b→ +d→ =(6; -4; -3); u→ =(1;m;2)

u ⃗⊥(b→ +d ⃗ )⇔u→ .(b→ +d→ )=0⇔6-4m-6=0⇔m=0

(u→ ,a→ )=600⇔cos⁡(u→ ,a→ )=1/2

Bài 2: Trong không gian hệ tọa độ Oxyz, cho hai vecto a→,b→ sao cho (a→,b→ )=1200,

|a→ |=2; |b→ |=3. Tính |a→+ b→ | và |a→-2b→ |

Áp dụng công thức: a→ .b→ =|a→ |.|b→ |.cos⁡(a→ ,b→ )

Ta có: |a→ + b→ |2=(a→ + b→ )2=a→ 2+2a→ .b→ +b→ 2

=|a→ |2+|b→ |2+2|a→ |.|b→ |.cos⁡(a→ ,b→ )=4+9+2.2.3.((-1)/2)=7

|a→ -2b→ |2 =|a→ |2+4|b→ |2-4|a→ |.|b→ |.cos⁡(a→ ,b→ )=4+36-4.2.3.((-1)/2)=52

Bài 3: Trong không gian Oxyz, cho các điểm A(2; -1; 1), B(3; 5; 2), C(8; 4; 3), D(-2; 2m+1; -3)

a) Chứng minh tam giác ABC là tam giác vuông

b) Tìm m sao cho tam giác ABD vuông tại A

c) Tính số đo góc A của tam giác ABC

a) Ta có: AB→=(1;6;1); BC→=(5;-1;1)

b) AB→=(1;6;1); AD→=(-4;2m+2; -4)

Tam giác ABD vuông tại A ⇔AB→.AD→=0

Bài 1: Cho các vectơ u→(u1;u2;u3) và v→(v1;v2;v3), u→. v→=0 khi và chỉ khi:

Bài 2: Cho hai vectơ a→ và b→ tạo với nhau góc 600 và |a→| =2; |b→| =4. Khi đó |a→ + b→ | bằng:

|a→ + b→ |2=(a→ + b→ )2=|a→ |2+|b→ |2+2|a→ |.|b→ |.cos⁡(a→ + b→ )

Bài 3: Cho a→(-2;1;3), b→(1;2;m). Với giá trị nào của m để a→ vuông góc với b→ ?

a→ vuông góc với b→ khi và chỉ khi a→ . b→=0

Bài 4: Tính cosin của góc giữa hai vectơ a→ và b→ biết a→(8;4;1), b→(2;-2;1)

Bài 5: Cho tam giác ABC với A(-1;-2;4), B(-4;-2;0), C(3;-2;1). Khi đó số đo của góc BACˆ bằng:

Bài 6: Cho bốn điểm A(1;0;0), B(0;1;0), C(0;0;1), D(-2;1;-1). Khi đó số đo của góc giữa hai đường thẳng AB và CD là :

Gọi góc giữa 2 đường thẳng AB và CD là α

Bài 7: Trong không gian với hệ toạ độ Oxyz, cho hai vecto a→; b→. Trong các khẳng định sau, khẳng định nào đúng:

A. a→ .|b→ |=|a→ |.b→ với mọi a→ ; b→

B. ( a→ b→ )2=a→ 2 . b→ 2 với mọi a→ ; b→

C. |a→ . b→ | ≤|a→ |.|b→ | với mọi a→ ; b→

D. a→ . b→ =0 khi và chỉ khi a→ = 0→ hoặc b→ = 0→

d) a→ b→ =0 nhưng a→ ≠ 0→ hoặc b→ ≠ 0→

Bài 8: Trong không gian Oxyz, cho a→(-1;2;-3), b→(3;3;4), c→(5;0-1). Giá trị của a→ (b→ + c→ ) là:

⇒ a→ (b→ + c→ )=-1.8+2.3-3.3=-11

Bài 9: Cho 3 điểm A(2; 1; -3), B(–2; 2; –6), C(5; 0; –1). Tích AB→. AC→ bằng:

⇒ AB→ . AC→ =-4.3+1.(-1)-3.2=-19

Bài 10: Trong không gian với hệ tọa độ Oxyz, điều kiện để a→ vuông góc với b→ là gì ?

A. a→ . b→ =0   B. [ a→ , b→] = 0→

C. a→ + b→ = 0→   D. a→ - b→ = 0→

Bài 11: Cho hai vecto a→; b→thay đổi nhưng luôn thỏa mãn |a→|=5; |b→ |=3. Giá trị lớn nhất của |a→ -2 b→ | là:

Ta có: |a→ - 2 b→ |2 = ( a→ - 2 b→ )2 = | a→ |2 + 4| b→ |2 - 4| a→ |.| b→ |.cos⁡( a→ ; b→ )

| a→ -2 b→ | lớn nhất ⇔ | a→ - 2 b→ |2 lớn nhất ⇔cos⁡( a→ ; b→ )=0

Khi đó: | a→ - 2 b→ |2=| a→ |2+4| b→ |2=25+4.9=61

Bài 12: Trong không gian với hệ toạ độ Oxyz, cho ba vectơ a→(-1;1;0), b→(1;1;0), c→(1;1;1,). Trong các mệnh đề sau, mệnh đề nào sai ?

⇒ Hai vecto c→ ; b→ không vuông góc với nhau

Bài 13: Trong không gian với hệ toạ độ Oxyz, cho tam giác ABC có AB→=(-3;0;4), AC→=(5;-2;4). Độ dài trung tuyến AM là:

Ta có: AB=|AB→ |=5; AC=|AC→ |=√45

Ta có: BC2=AB2+AC2 - 2AB.AC.cos⁡BACˆ =68

Bài 14: Cho | a→ |=2; | b→ |=5, góc giữa hai vectơ a→ và b→ bằng (2π)/3, u→ = k a→ - b→; v→ = a→ + 2 b→. Để u→ vuông góc với v→ thì k bằng?

⇒ u→ . v→ =(k a→ - b→ )(a→ +2 b→ )=k a→ 2-2 b→ 2+(2k-1) a→ . b→

Ta có: a→ . b→ =| a→ |.| b→ |.cos⁡( a→ ; b→ )=2.5.cos⁡(2π/3)=-5

⇒ u→ . v→ =4k-2.25+(2k-1).(-5)=-6k-45

Giả thiết: u→ và v→ vuông góc với nhau ⇒ u→ . v→ =0

Bài 15: Trong không gian với hệ tọa độ Oxyz, cho a→=(x;2;1), b→ =(2;1;2), Tìm x biết cos( a→ , b→ )=2/3.

Bài 16: Trong không gian với hệ tọa độ Oxyz, cho A→ (-2;2;-1), B→ (-2;3;0), C→ (x;3;-1). Giá trị của x để tam giác ABC đều là:

AB→ =(0;1;1); AC→ =(x+2;1;0); BC→ =(x+2;0;-1)

Tam giác ABC đều ⇔ BACˆ= ABCˆ=600

Bài 17: Cho hai vecto a→; b→ tạo với nhau một góc 600. Biết độ dài của hai vecto đó lần lượt là 5 và 10. Độ dài của vecto hiệu a→ - b→ là:

Ta có: | a→ - b→ |2=( a→ - b→ )2=| a→ |2+| b→ |2-2| a→ |.| b→ |.cos⁡( a→ ; b→ )

Bài 18: Trong không gian với hệ tọa độ Oxyz,cho tam giác ABC với A(-4;3;5), B(-3;2;5) và C(5;-3;8). Tính cos⁡(AB→ ; BC→ ).

AB→ =(1; -1;0); BC→ =(8; -5;3)

Bài 19: Trong không gian với hệ toạ độ Oxyz, tam giác ABC có A(-1;-2;4), B(-4;-2;0), C(3;-2;1). Số đo của góc B là:

Bài 20: Trong không gian Oxyz, cho hai điểm A(x; y; z), B(m, n, p) thay đổi nhưng luôn thỏa mãn điều kiện x2+y2+z2=4; m2+n2+p2=9. Vecto AB→ có độ dài nhỏ nhất là:

Dấu bằng xảy ra khi O nằm ngoài đoạn AB.

ĐỀ THI, GIÁO ÁN, GÓI THI ONLINE DÀNH CHO GIÁO VIÊN VÀ PHỤ HUYNH LỚP 12

Bộ giáo án, đề thi, bài giảng powerpoint, khóa học dành cho các thầy cô và học sinh lớp 12, đẩy đủ các bộ sách cánh diều, kết nối tri thức, chân trời sáng tạo tại https://tailieugiaovien.com.vn/ . Hỗ trợ zalo VietJack Official

phuong-phap-toa-do-trong-khong-gian.jsp

Giải bài tập lớp 12 sách mới các môn học

A. Tồn tại ba số thực m, n, p thoả mãn m+n+p=0 và ma→+nb→+pc→=0

(HQ Online) - Ngày 2/11, tại Văn phòng Quân ủy Trung ương, Đại tướng Phan Văn Giang, Ủy viên Bộ Chính trị, Phó Bí thư Quân ủy Trung ương, Bộ trưởng Bộ Quốc phòng đã trao Quyết định số 420/QĐĐ-BQP và Quyết định số 468/QĐĐ-BQP ngày 1/11/2024 về việc bổ nhiệm cán bộ cho Thượng tá Cao Anh Sơn và Trung tá Nguyễn Đạt giữ chức vụ Phó Tổng Giám đốc Tập đoàn Công nghiệp - Viễn thông Quân đội (Viettel).

Trước đó, ban lãnh đạo Viettel gồm Chủ tịch kiêm Tổng giám đốc Tập đoàn – Thiếu tướng Tào Đức Thắng; Bí thư Đảng uỷ, Phó Tổng Giám đốc – Thiếu tướng Nguyễn Đình Chiến; các Phó Tổng Giám đốc: Thiếu tướng Đỗ Minh Phương, Đại tá Đào Xuân Vũ.

Thượng tá Cao Anh Sơn sinh năm 1975, bắt đầu làm việc tại Viettel từ năm 2000 ở vị trí kỹ sư phòng Kỹ thuật.

Trong 24 năm gắn bó, ông Sơn đã trải qua nhiều vị trí quan trọng như Trưởng phòng Tính cước, Giám đốc Trung tâm Kinh doanh Quốc tế của TCT Viễn thông Viettel, Phó Trưởng ban Công nghệ Thông tin Tập đoàn, Phó Tổng giám đốc TCT CP Đầu tư Quốc tế Viettel (VTG), Tổng Giám đốc Công ty Viettel Star Telecom (Unitel). Trước khi được bổ nhiệm, ông Sơn là Tổng giám đốc TCT Viễn thông Viettel (VTT).

Trung tá Nguyễn Đạt sinh năm 1981, hiện là thành viên trẻ nhất trong Ban TGĐ Tập đoàn.

Ông Đạt gia nhập Viettel từ năm 2008, kinh qua nhiều vị trí, từ nhân sự về quản trị hệ thống đến cán bộ quản lý, giữ các chức vụ quan trọng. Ông Đạt đã 2 lần giữ chức vụ Trưởng ban Kỹ thuật Tập đoàn, 2 lần đảm nhiệm vị trí người đứng đầu TCT Mạng lưới Viettel (VTNet).

Ông Đạt cũng từng giữ chức vụ Tổng Giám đốc Movitel (Viettel Mozambique) và Tổng Giám đốc TCT CP Đầu tư quốc tế (VTG). Ông Đạt là Tổng Giám đốc TCT Mạng lưới trước khi được bổ nhiệm PTGĐ Tập đoàn Viettel.

Tập đoàn Công nghiệp - Viễn thông Quân đội (Viettel) vừa có thêm hai Phó tổng giám đốc là ông Cao Anh Sơn và Nguyễn Đạt.

Bộ trưởng Quốc phòng Phan Văn Giang trao quyết định bổ nhiệm hai Phó tổng giám đốc Tập đoàn Viettel ngày 2/11. Theo đó, Thượng tá Cao Anh Sơn và Trung tá Nguyễn Đạt sẽ giữ chức vụ này từ ngày 1/11.

Ông Cao Anh Sơn (thứ hai từ bên trái) và ông Nguyễn Đạt (thứ hai từ bên phải) vừa được bổ nhiệm làm Phó tổng giám đốc Tập đoàn Viettel. Ảnh: VT

Ông Sơn sinh năm 1975, bắt đầu làm việc tại Viettel từ năm 2000 với vị trí kỹ sư phòng kỹ thuật. Trong 24 năm gắn bó tập đoàn, ông Sơn đã trải qua nhiều vị trí như Trưởng phòng tính cước, Giám đốc Trung tâm Kinh doanh Quốc tế của Tổng công ty Viettel Telecom, Phó trưởng ban Công nghệ thông tin tập đoàn, Phó tổng giám đốc Viettel Global, Tổng giám đốc Viettel Star Telecom (Unitel). Trước khi được bổ nhiệm làm phó tổng giám đốc Tập đoàn Viettel, ông Sơn giữ vai trò Tổng giám đốc Viettel Telecom.

Trung tá Nguyễn Đạt sinh năm 1981 - hiện là thành viên trẻ nhất trong Ban tổng giám đốc tập đoàn này. Ông Đạt gia nhập Viettel từ năm 2008 và cũng trải qua nhiều vị trí từ nhân sự về quản trị hệ thống đến cán bộ quản lý. Ông có 2 lần làm Trưởng ban Kỹ thuật Tập đoàn Viettel. Ông cũng từng giữ chức Tổng giám đốc Movitel (Viettel Mozambique) và Tổng giám đốc Viettel Global. Vị trí gần nhất của ông Đạt là Tổng giám đốc Viettel Networks.

Như vậy, sau khi bổ nhiệm thêm 2 thành viên mới, ban lãnh đạo của tập đoàn Viettel có 6 thành viên, trong đó Chủ tịch, kiêm Tổng giám đốc là Thiếu tướng Tào Đức Thắng. 3 thành viên cũ khác là Thiếu tướng Nguyễn Đình Chiến, Bí thư Đảng uỷ, kiêm Phó tổng giám đốc; Thiếu tướng Đỗ Minh Phương và Đại tá Đào Xuân Vũ cũng là Phó tổng giám đốc.